一、参考文档:
https://blog.csdn.net/lxbhahaha/article/details/111687476
https://blog.csdn.net/qq_38523017/article/details/108885870
https://github.com/yiwei151/PolygonTriangulation
https://zhuanlan.zhihu.com/p/368191630
https://www.geometrictools.com/Documentation/TriangulationByEarClipping.pdf
二、适用情景
此方法只适用于不带岛洞的简单多边形绘制,但是如果是绘制复杂多边形则会返回null。
下图中只有第一种是简单多边形,其余两种则不是。
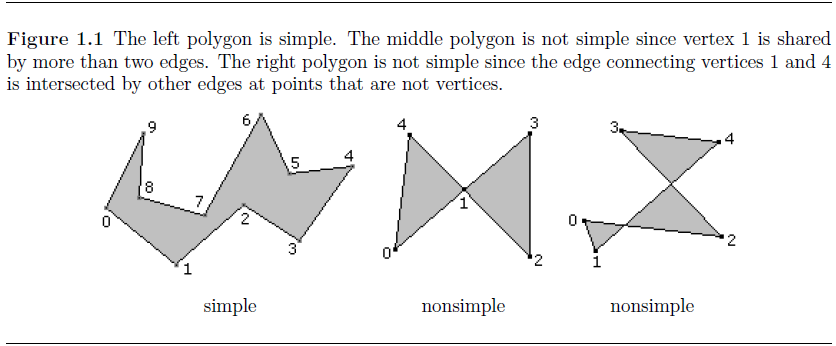
三、耳切法解释
算法简介:将一个简单多边分解成三角形集合的方法称之为多边形的三角形化(triangulation of the Polygon)。几何学的知识告诉我们,由n个顶点组成的简单多边形总是可以分解成n -2个三角形。最简单的算法就是耳切法,时间复杂度为 O(n²)。具体算法是找出n个顶点简单多边形的一个耳朵来构造一个三角形,并将这个耳朵的耳尖从简单多边形的顶点数组中剔除,剩下的n-1个顶点形成了一个新的简单多边形。递归执行上一步直到剩下2个顶点为止(因为构成一个三角形最少需要3个顶点),这样就把这样一个简单多边形构造成了一组三角形。
名词解释:
简单多边形:简单多边形是指由一组有序顶点组成的,点V0~点Vn-1。相邻的顶点之间通过边(Vi, Vi-1)连接,并且边(Vn-1,V0)连接起始点。每个顶点被两条边所共享,而边的所有交点都是顶点。
岛洞:简单理解就是多边形的镂空
耳朵:由连续顶点Vi-1,Vi和Vi+1组成的内部不包含其他任意顶点的三角形,其中Vi称为耳尖。
四、算法代码
函数是传入一个多边形顶点的List(按照我的需求多边形顶点给的是逆时针为顺序,并且是一个位于xOz平面上的多边形,所以比较轴我也设置的Y轴),然后返回对应三角形的索引。
using System;
using System.Collections.Generic;
using UnityEngine;
namespace PolygonTool
{
#region 耳切法对简单多边形进行三角形化
/// <summary>
/// 判断凹点,凸点,耳朵的比较轴
/// </summary>
public enum CompareAxle
{
X,
Y,
Z
}
/// <summary>
/// 对多边形处理
/// </summary>
public class Triangulation
{
/// <summary>
/// 判断凹凸的时候的比对轴
/// </summary>
private CompareAxle _compareAxle = CompareAxle.Y;
/// <summary>
/// 多边形顶点
/// </summary>
private List<Vector3> _polygonVertexs = new List<Vector3>();
/// <summary>
/// 顶点序列
/// </summary>
private List<int> _vertexsSequence = new List<int>();
/// <summary>
/// 节点管理器
/// </summary>
private NodeManager _nodeManager = new NodeManager();
/// <summary>
/// 初始化
/// </summary>
/// <param name="polygonVertexs">多边形顶点</param>
public Triangulation(List<Vector3> polygonVertexs)
{
this._polygonVertexs = polygonVertexs;
_nodeManager.Init(polygonVertexs);
}
/// <summary>
/// 设置比较轴
/// </summary>
/// <param name="compareAxle"></param>
public void SetCompareAxle(CompareAxle compareAxle)
{
this._compareAxle = compareAxle;
}
/// <summary>
/// 获取三角形的顶点序列
/// </summary>
public int[] GetTriangles()
{
while (_nodeManager.LinkedListLength >= 3)
{
SplitResult sr = SplitPolygon();
//
if (sr == null)
{
Debug.Log("null");
return null;
}
}
return _vertexsSequence.ToArray();
}
/// <summary>
/// 计算凹顶点,凸顶点,耳朵
/// </summary>
private SplitResult SplitPolygon()
{
//凹点
List<Node> _concaveVertexs = new List<Node>();
//凸点
List<Node> _raisedVertexs = new List<Node>();
//耳朵
List<Node> _polygonEars = new List<Node>();
//起始节点
Node currentNode = _nodeManager.FirstNode;
#region 计算凹顶点,凸顶点
for (int i = 0; i < _nodeManager.LinkedListLength; i++)
{
Vector3 one = currentNode.vertex - currentNode.lastNode.vertex;
Vector3 two = currentNode.nextNode.vertex - currentNode.vertex;
Vector3 crossRes = Vector3.Cross(one, two);
if (_compareAxle == CompareAxle.Y)
{
if (crossRes.y > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
if (_compareAxle == CompareAxle.X)
{
if (crossRes.x > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
if (_compareAxle == CompareAxle.Z)
{
if (crossRes.z > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
_polygonEars.Add(currentNode);
currentNode = currentNode.nextNode;
}
for (int i = 0; i < _concaveVertexs.Count; i++)
{
_polygonEars.Remove(_concaveVertexs[i]);
}
#endregion
#region 计算耳朵
List<int> needRemoveIdList = new List<int>();
for (int i = 0; i < _polygonEars.Count; i++)
{
Node earNode = _polygonEars[i];
Node compareNode = earNode.nextNode.nextNode;
while (compareNode != earNode.lastNode)
{
bool isIn = IsIn(compareNode.vertex, earNode.lastNode.vertex, earNode.vertex,
earNode.nextNode.vertex);
if (isIn == true)
{
if (_polygonEars.Contains(_polygonEars[i]))
{
needRemoveIdList.Add(_polygonEars[i].id);
}
break;
}
compareNode = compareNode.nextNode;
}
}
for (int j = 0; j < needRemoveIdList.Count; j++)
{
for (int i = 0; i < _polygonEars.Count; i++)
{
if (_polygonEars[i].id == needRemoveIdList[j])
{
_polygonEars.RemoveAt(i);
}
}
}
#endregion
#region 打印初始化结果
Debug.Log("凸点");
for (int i = 0; i < _raisedVertexs.Count; i++)
{
Debug.Log(_raisedVertexs[i].id);
}
Debug.Log("凹点");
for (int i = 0; i < _concaveVertexs.Count; i++)
{
Debug.Log(_concaveVertexs[i].id);
}
Debug.Log("耳朵");
for (int i = 0; i < _polygonEars.Count; i++)
{
Debug.Log(_polygonEars[i].id);
}
Debug.Log("-----------------------------------------------");
#endregion
//耳朵为空说明不是简单多边形 多边形三角化失败
if (_polygonEars.Count == 0)
{
return null;
}
_vertexsSequence.Add(_polygonEars[0].lastNode.id);
_vertexsSequence.Add(_polygonEars[0].id);
_vertexsSequence.Add(_polygonEars[0].nextNode.id);
_nodeManager.RemoveNode(_polygonEars[0]);
return new SplitResult(_raisedVertexs, _concaveVertexs, _polygonEars);
}
/// <summary>
/// 判断一点是否在三角形内
/// </summary>
/// <param name="p">一点</param>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="c"></param>
/// <returns></returns>
public bool IsIn(Vector3 p,Vector3 a,Vector3 b,Vector3 c)
{
Vector3 pa = p - a;
Vector3 pb = p - b;
Vector3 pc = p - c;
Vector3 t1 = Vector3.Cross(pa, pb);
Vector3 t2 = Vector3.Cross(pb, pc);
Vector3 t3 = Vector3.Cross(pc, pa);
bool isIn2 = t1.y >= 0 && t2.y >= 0 && t3.y >= 0 || t1.y <= 0 && t2.y <= 0 && t3.y <= 0;
return isIn2;
}
/// <summary>
/// 管理多边形 构成一个双向链表
/// </summary>
public class NodeManager
{
private List<Node> _nodeList = new List<Node>();
public int LinkedListLength
{
get { return _nodeList.Count; }
}
public Node FirstNode
{
get { return _nodeList[0]; }
}
public void Init(List<Vector3> vertexs)
{
for (int i = 0; i < vertexs.Count; i++)
{
Node node = new Node(i, vertexs[i]);
_nodeList.Add(node);
}
for (int i = 0; i < LinkedListLength; i++)
{
if (i == 0)
{
_nodeList[i].lastNode = _nodeList[LinkedListLength - 1];
_nodeList[i].nextNode = _nodeList[1];
}
else if (i == LinkedListLength - 1)
{
_nodeList[i].lastNode = _nodeList[LinkedListLength - 2];
_nodeList[i].nextNode = _nodeList[0];
}
else
{
_nodeList[i].lastNode = _nodeList[i - 1];
_nodeList[i].nextNode = _nodeList[i + 1];
}
}
}
public void RemoveNode(Node node)
{
_nodeList.Remove(node);
node.lastNode.nextNode = node.nextNode;
node.nextNode.lastNode = node.lastNode;
}
}
public class Node
{
public int id;
public Vector3 vertex;
public Node lastNode;
public Node nextNode;
public Node(int id, Vector3 vertex)
{
this.id = id;
this.vertex = vertex;
}
public Node(int id, Vector3 vertex, Node lastNode, Node nextNode)
{
this.id = id;
this.vertex = vertex;
this.lastNode = lastNode;
this.nextNode = nextNode;
}
}
public class SplitResult
{
/// <summary>
/// 凸顶点
/// </summary>
public List<Node> raisedVertexs;
/// <summary>
/// 凹顶点
/// </summary>
public List<Node> concaveVertexs;
/// <summary>
/// 耳朵
/// </summary>
public List<Node> polygonEars;
public SplitResult(List<Node> raisedVertexs, List<Node> concaveVertexs, List<Node> polygonEars)
{
this.raisedVertexs = raisedVertexs;
this.concaveVertexs = concaveVertexs;
this.polygonEars = polygonEars;
}
}
}
#endregion
}
五、测试代码
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using PolygonTool;
public class T : MonoBehaviour
{
//用物体的坐标来代替点
public List<Transform> tList;
//计算得到的三角形序列下标
private List<int> resultList = new List<int>();
private Triangulation triangulation;
private void Start()
{
tList.Reverse();
List<Vector3> posList = new List<Vector3>();
for (int i = 0; i < tList.Count; i++)
{
posList.Add(tList[i].position);
}
triangulation = new Triangulation(posList);
triangulation.SetCompareAxle(CompareAxle.Y);
int[] a = triangulation.GetTriangles();
if (a != null)
{
for (int i = 0; i < a.Length; i++)
{
Debug.Log("===:" + a[i]);
resultList.Add(a[i]);
}
}
GameObject go = new GameObject();
MeshFilter mf = go.AddComponent<MeshFilter>();
go.AddComponent<MeshRenderer>();
Mesh m = new Mesh();
Vector3[] vertexs = new Vector3[a.Length];
for (int i = 0; i < vertexs.Length; i++)
{
Vector3 v = tList[a[i]].position;
vertexs[i] = v;
}
m.vertices = vertexs;
int[] tri = new int[a.Length];
for (int i = 0; i < tri.Length; i += 3)
{
tri[i] = i;
tri[i + 1] = i + 2;
tri[i + 2] = i + 1;
}
m.triangles = tri;
mf.mesh = m;
}
private void OnDrawGizmos()
{
for (int i = 0; i < tList.Count; i++)
{
if (i < tList.Count - 1)
{
Gizmos.DrawLine(tList[i].position, tList[i + 1].position);
}
else
{
Gizmos.DrawLine(tList[i].position, tList[0].position);
}
}
Gizmos.color = Color.black;
for (int i = 0; i < resultList.Count; i+=3)
{
int startIndex = resultList[i];
int endIndex = resultList[i + 2];
Gizmos.DrawLine(tList[startIndex].position, tList[endIndex].position);
}
}
}
